Publications
Publications in reverse chronological order.
2025
- The Future of Artificial Intelligence and the Mathematical and Physical Sciences (AI+MPS)Andrew Ferguson, Marisa LaFleur, Lars Ruthotto, Jesse Thaler, Yuan-Sen Ting, Pratyush Tiwary, Soledad Villar, E. Paulo Alves, Jeremy Avigad, Simon Billinge, Camille Bilodeau, Keith Brown, and 88 more authors2025
This community paper developed out of the NSF Workshop on the Future of Artificial Intelligence (AI) and the Mathematical and Physics Sciences (MPS), which was held in March 2025 with the goal of understanding how the MPS domains (Astronomy, Chemistry, Materials Research, Mathematical Sciences, and Physics) can best capitalize on, and contribute to, the future of AI. We present here a summary and snapshot of the MPS community’s perspective, as of Spring/Summer 2025, in a rapidly developing field. The link between AI and MPS is becoming increasingly inextricable; now is a crucial moment to strengthen the link between AI and Science by pursuing a strategy that proactively and thoughtfully leverages the potential of AI for scientific discovery and optimizes opportunities to impact the development of AI by applying concepts from fundamental science. To achieve this, we propose activities and strategic priorities that: (1) enable AI+MPS research in both directions; (2) build up an interdisciplinary community of AI+MPS researchers; and (3) foster education and workforce development in AI for MPS researchers and students. We conclude with a summary of suggested priorities for funding agencies, educational institutions, and individual researchers to help position the MPS community to be a leader in, and take full advantage of, the transformative potential of AI+MPS.
-
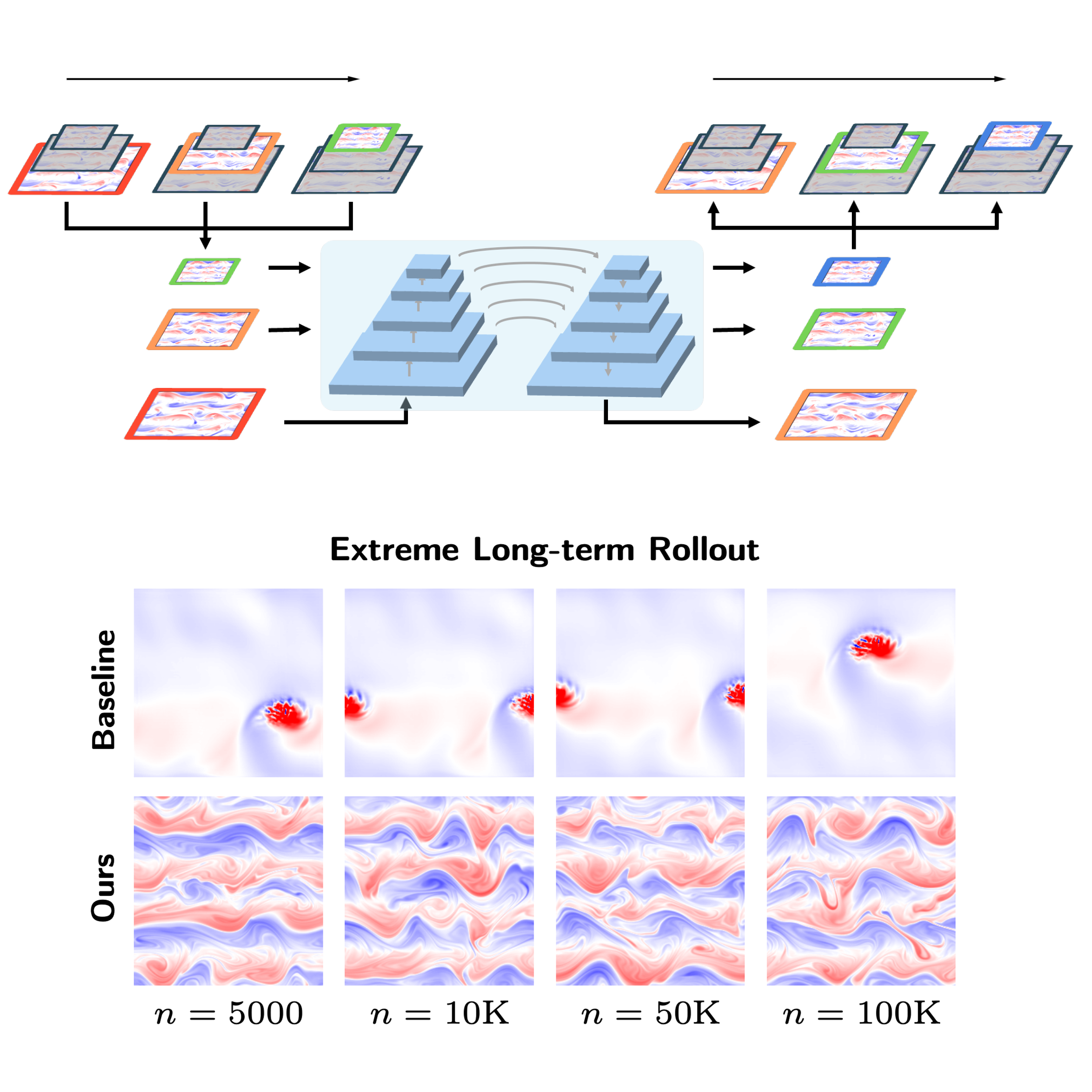 Hierarchical Implicit Neural EmulatorsRuoxi Jiang, Xiao Zhang, Karan Jakhar, Peter Y. Lu, Pedram Hassanzadeh, Michael Maire, and Rebecca WillettIn Thirty-ninth Conference on Neural Information Processing Systems, 2025
Hierarchical Implicit Neural EmulatorsRuoxi Jiang, Xiao Zhang, Karan Jakhar, Peter Y. Lu, Pedram Hassanzadeh, Michael Maire, and Rebecca WillettIn Thirty-ninth Conference on Neural Information Processing Systems, 2025Neural PDE solvers offer a powerful tool for modeling complex dynamical systems, but often struggle with error accumulation over long time horizons and maintaining stability and physical consistency. We introduce a multiscale implicit neural emulator that enhances long-term prediction accuracy by conditioning on a hierarchy of lower-dimensional future state representations. Drawing inspiration from the stability properties of numerical implicit time-stepping methods, our approach leverages predictions several steps ahead in time at increasing compression rates for next-timestep refinements. By actively adjusting the temporal downsampling ratios, our design enables the model to capture dynamics across multiple granularities and enforce long-range temporal coherence. Experiments on turbulent fluid dynamics show that our method achieves high short-term accuracy and produces long-term stable forecasts, significantly outperforming autoregressive baselines while adding minimal computational overhead.
-
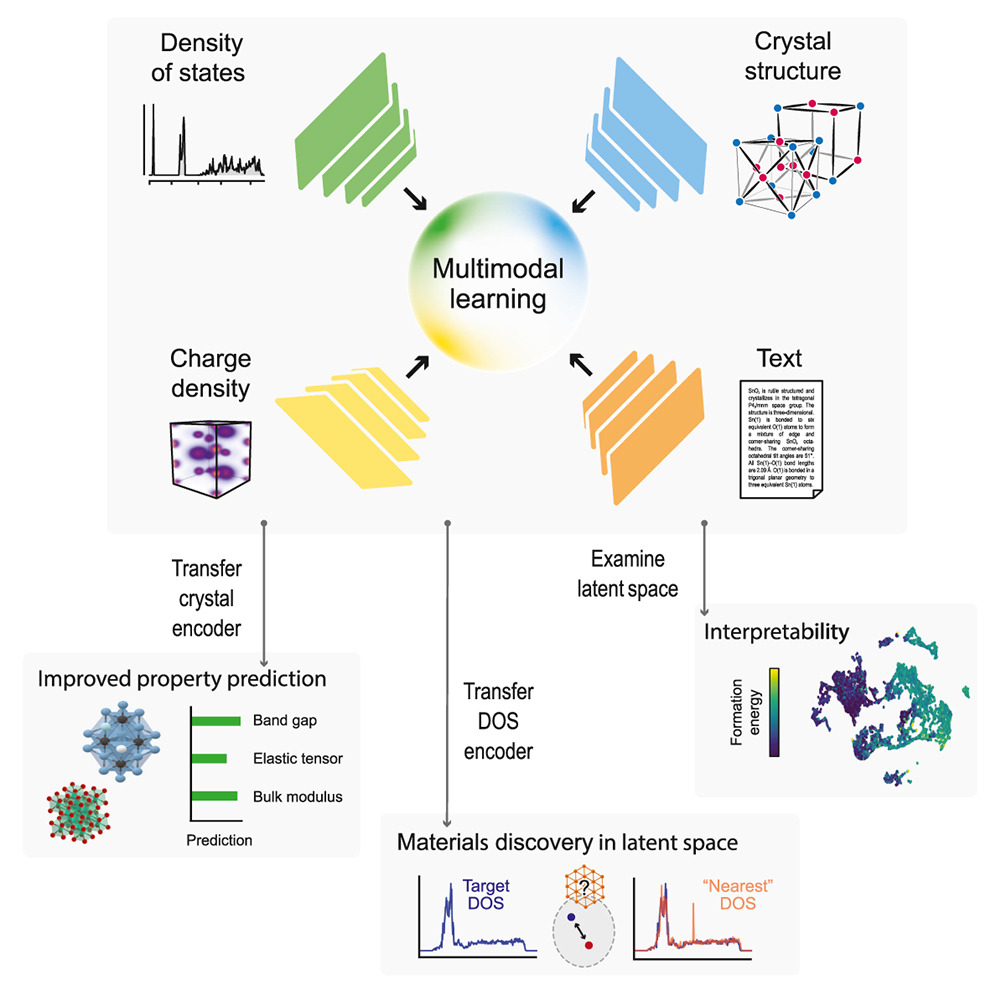 Multimodal foundation models for material property prediction and discoveryViggo Moro, Charlotte Loh, Rumen Dangovski, Ali Ghorashi, Andrew Ma, Zhuo Chen, Samuel Kim, Peter Y. Lu, Thomas Christensen, and Marin SoljačićNewton, 2025
Multimodal foundation models for material property prediction and discoveryViggo Moro, Charlotte Loh, Rumen Dangovski, Ali Ghorashi, Andrew Ma, Zhuo Chen, Samuel Kim, Peter Y. Lu, Thomas Christensen, and Marin SoljačićNewton, 2025Artificial intelligence is transforming computational materials science by improving property prediction and accelerating the discovery of novel materials. Recently, publicly available material data repositories have grown rapidly, encompassing not only more materials but also a greater variety and quantity of their associated properties. Existing machine-learning efforts in materials science focus primarily on single-modality tasks, i.e., relationships between materials and a single physical property, thus not taking advantage of the rich multimodal data available. Here, we introduce multimodal learning for materials (MultiMat), a framework enabling self-supervised multimodal training of foundation models for materials. Using the Materials Project database, we demonstrate the potential of MultiMat by: (1) achieving state-of-the-art performance for challenging material property prediction tasks; (2) enabling novel and accurate material discovery via latent-space similarity, allowing screening for stable materials with desired properties; and (3) encoding emergent features that correlate with material properties and may provide novel scientific insights.
2024
- Embed and Emulate: Contrastive representations for simulation-based inferenceRuoxi Jiang*, Peter Y. Lu*, and Rebecca Willett2024
Scientific modeling and engineering applications rely heavily on parameter estimation methods to fit physical models and calibrate numerical simulations using real-world measurements. In the absence of analytic statistical models with tractable likelihoods, modern simulation-based inference (SBI) methods first use a numerical simulator to generate a dataset of parameters and simulated outputs. This dataset is then used to approximate the likelihood and estimate the system parameters given observation data. Several SBI methods employ machine learning emulators to accelerate data generation and parameter estimation. However, applying these approaches to high-dimensional physical systems remains challenging due to the cost and complexity of training high-dimensional emulators. This paper introduces Embed and Emulate (E&E): a new SBI method based on contrastive learning that efficiently handles high-dimensional data and complex, multimodal parameter posteriors. E&E learns a low-dimensional latent embedding of the data (i.e., a summary statistic) and a corresponding fast emulator in the latent space, eliminating the need to run expensive simulations or a high dimensional emulator during inference. We illustrate the theoretical properties of the learned latent space through a synthetic experiment and demonstrate superior performance over existing methods in a realistic, non-identifiable parameter estimation task using the high-dimensional, chaotic Lorenz 96 system.
- Deep Stochastic MechanicsIn Proceedings of the 41st International Conference on Machine Learning, 2024
This paper introduces a novel deep-learning-based approach for numerical simulation of a time-evolving Schrödinger equation inspired by stochastic mechanics and generative diffusion models. Unlike existing approaches, which exhibit computational complexity that scales exponentially in the problem dimension, our method allows us to adapt to the latent low-dimensional structure of the wave function by sampling from the Markovian diffusion. Depending on the latent dimension, our method may have far lower computational complexity in higher dimensions. Moreover, we propose novel equations for stochastic quantum mechanics, resulting in quadratic computational complexity with respect to the number of dimensions. Numerical simulations verify our theoretical findings and show a significant advantage of our method compared to other deep-learning-based approaches used for quantum mechanics.
- Deep Learning and Symbolic Regression for Discovering Parametric EquationsMichael Zhang, Samuel Kim, Peter Y. Lu, and Marin SoljačićIEEE Transactions on Neural Networks and Learning Systems, 2024
Symbolic regression is a machine learning technique that can learn the equations governing data and thus has the potential to transform scientific discovery. However, symbolic regression is still limited in the complexity and dimensionality of the systems that it can analyze. Deep learning, on the other hand, has transformed machine learning in its ability to analyze extremely complex and high-dimensional datasets. We propose a neural network architecture to extend symbolic regression to parametric systems where some coefficient may vary, but the structure of the underlying governing equation remains constant. We demonstrate our method on various analytic expressions and partial differential equations (PDEs) with varying coefficients and show that it extrapolates well outside of the training domain. The proposed neural-network-based architecture can also be enhanced by integrating with other deep learning architectures such that it can analyze high-dimensional data while being trained end-to-end. To this end, we demonstrate the scalability of our architecture by incorporating a convolutional encoder to analyze 1-D images of varying spring systems.
2023
-
 Training neural operators to preserve invariant measures of chaotic attractorsIn Thirty-seventh Conference on Neural Information Processing Systems, 2023
Training neural operators to preserve invariant measures of chaotic attractorsIn Thirty-seventh Conference on Neural Information Processing Systems, 2023Chaotic systems make long-horizon forecasts difficult because small perturbations in initial conditions cause trajectories to diverge at an exponential rate. In this setting, neural operators trained to minimize squared error losses, while capable of accurate short-term forecasts, often fail to reproduce statistical or structural properties of the dynamics over longer time horizons and can yield degenerate results. In this paper, we propose an alternative framework designed to preserve invariant measures of chaotic attractors that characterize the time-invariant statistical properties of the dynamics. Specifically, in the multi-environment setting (where each sample trajectory is governed by slightly different dynamics), we consider two novel approaches to training with noisy data. First, we propose a loss based on the optimal transport distance between the observed dynamics and the neural operator outputs. This approach requires expert knowledge of the underlying physics to determine what statistical features should be included in the optimal transport loss. Second, we show that a contrastive learning framework, which does not require any specialized prior knowledge, can preserve statistical properties of the dynamics nearly as well as the optimal transport approach. On a variety of chaotic systems, our method is shown empirically to preserve invariant measures of chaotic attractors.
- Discovering conservation laws using optimal transport and manifold learningPeter Y. Lu, Rumen Dangovski, and Marin SoljačićNature Communications, 2023
Conservation laws are key theoretical and practical tools for understanding, characterizing, and modeling nonlinear dynamical systems. However, for many complex systems, the corresponding conserved quantities are difficult to identify, making it hard to analyze their dynamics and build stable predictive models. Current approaches for discovering conservation laws often depend on detailed dynamical information or rely on black box parametric deep learning methods. We instead reformulate this task as a manifold learning problem and propose a non-parametric approach for discovering conserved quantities. We test this new approach on a variety of physical systems and demonstrate that our method is able to both identify the number of conserved quantities and extract their values. Using tools from optimal transport theory and manifold learning, our proposed method provides a direct geometric approach to identifying conservation laws that is both robust and interpretable without requiring an explicit model of the system nor accurate time information.
- Q-Flow: Generative Modeling for Differential Equations of Open Quantum Dynamics with Normalizing FlowsIn Proceedings of the 40th International Conference on Machine Learning, 2023
Studying the dynamics of open quantum systems can enable breakthroughs both in fundamental physics and applications to quantum engineering and quantum computation. Since the density matrix ρ, which is the fundamental description for the dynamics of such systems, is high-dimensional, customized deep generative neural networks have been instrumental in modeling ρ. However, the complex-valued nature and normalization constraints of ρ, as well as its complicated dynamics, prohibit a seamless connection between open quantum systems and the recent advances in deep generative modeling. Here we lift that limitation by utilizing a reformulation of open quantum system dynamics to a partial differential equation (PDE) for a corresponding probability distribution Q, the Husimi Q function. Thus, we model the Q function seamlessly with off-the-shelf deep generative models such as normalizing flows. Additionally, we develop novel methods for learning normalizing flow evolution governed by high-dimensional PDEs based on the Euler method and the application of the time-dependent variational principle. We name the resulting approach Q-Flow and demonstrate the scalability and efficiency of Q-Flow on open quantum system simulations, including the dissipative harmonic oscillator and the dissipative bosonic model. Q-Flow is superior to conventional PDE solvers and state-of-the-art physics-informed neural network solvers, especially in high-dimensional systems.
- Studying Phase Transitions in Contrastive Learning With Physics-Inspired DatasetsIn ICLR 2023 Workshop on Physics for Machine Learning, 2023
In recent years contrastive learning has become a state-of-the-art technique in representation learning, but the exact mechanisms by which it trains are not well understood. By focusing on physics-inspired datasets with low intrinsic dimensionality, we are able to visualize and study contrastive training procedures in better resolution. We empirically study the geometric development of contrastively learned embeddings, discovering phase transitions between locally metastable embedding conformations towards an optimal structure. Ultimately we show a strong experimental link between stronger augmentations and decreased training time for contrastively learning more geometrically meaningful representations.
2022
- Model Stitching: Looking For Functional Similarity Between RepresentationsIn NeurIPS 2022 Workshop on Shared Visual Representations in Human and Machine Intelligence, 2022
Model stitching (Lenc & Vedaldi 2015) is a compelling methodology to compare different neural network representations, because it allows us to measure to what degree they may be interchanged. We expand on a previous work from Bansal, Nakkiran & Barak which used model stitching to compare representations of the same shapes learned by differently seeded and/or trained neural networks of the same architecture. Our contribution enables us to compare the representations learned by layers with different shapes from neural networks with different architectures. We subsequently reveal unexpected behavior of model stitching. Namely, we find that stitching, based on convolutions, for small ResNets, can reach high accuracy if those layers come later in the first (sender) network than in the second (receiver), even if those layers are far apart.
- Deep Learning for Bayesian Optimization of Scientific Problems with High-Dimensional StructureTransactions of Machine Learning Research, 2022
Bayesian optimization (BO) is a popular paradigm for global optimization of expensive black-box functions, but there are many domains where the function is not completely a black-box. The data may have some known structure (e.g. symmetries) and/or the data generation process may be a composite process that yields useful intermediate or auxiliary information in addition to the value of the optimization objective. However, surrogate models traditionally employed in BO, such as Gaussian Processes (GPs), scale poorly with dataset size and do not easily accommodate known structure. Instead, we use Bayesian neural networks, a class of scalable and flexible surrogate models with inductive biases, to extend BO to complex, structured problems with high dimensionality. We demonstrate BO on a number of realistic problems in physics and chemistry, including topology optimization of photonic crystal materials using convolutional neural networks, and chemical property optimization of molecules using graph neural networks. On these complex tasks, we show that neural networks often outperform GPs as surrogate models for BO in terms of both sampling efficiency and computational cost.
- Discovering sparse interpretable dynamics from partial observationsPeter Y. Lu, Joan Ariño Bernad, and Marin SoljačićCommunications Physics, 2022
Identifying the governing equations of a nonlinear dynamical system is key to both understanding the physical features of the system and constructing an accurate model of the dynamics that generalizes well beyond the available data. Achieving this kind of interpretable system identification is even more difficult for partially observed systems. We propose a machine learning framework for discovering the governing equations of a dynamical system using only partial observations, combining an encoder for state reconstruction with a sparse symbolic model. The entire architecture is trained end-to-end by matching the higher-order symbolic time derivatives of the sparse symbolic model with finite difference estimates from the data. Our tests show that this method can successfully reconstruct the full system state and identify the equations of motion governing the underlying dynamics for a variety of ordinary differential equation (ODE) and partial differential equation (PDE) systems.
2021
- Discovering Dynamical Parameters by Interpreting Echo State NetworksOreoluwa Alao*, Peter Y. Lu*, and Marin SoljačićIn NeurIPS 2021 AI for Science Workshop, 2021
Reservoir computing architectures known as echo state networks (ESNs) have been shown to have exceptional predictive capabilities when trained on chaotic systems. However, ESN models are often seen as black-box predictors that lack interpretability. We show that the parameters governing the dynamics of a complex nonlinear system can be encoded in the learned readout layer of an ESN. We can extract these dynamical parameters by examining the geometry of the readout layer weights through principal component analysis. We demonstrate this approach by extracting the values of three dynamical parameters (σ, ρ, β) from a dataset of Lorenz systems where all three parameters are varying among different trajectories. Our proposed method not only demonstrates the interpretability of the ESN readout layer but also provides a computationally inexpensive, unsupervised data-driven approach for identifying uncontrolled variables affecting real-world data from nonlinear dynamical systems.
-
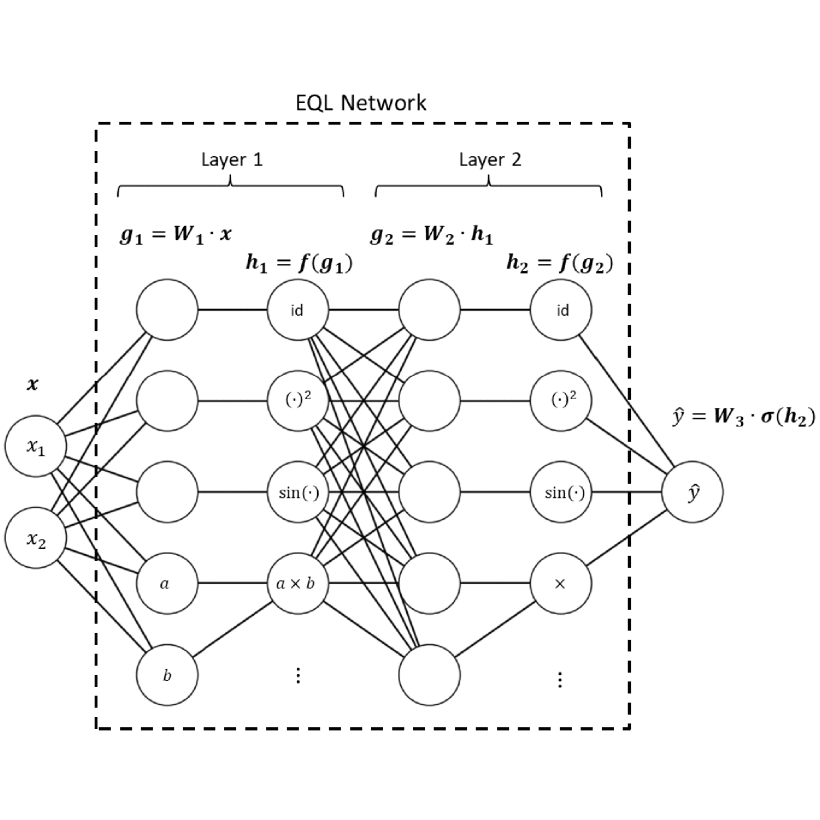 Integration of Neural Network-Based Symbolic Regression in Deep Learning for Scientific DiscoverySamuel Kim, Peter Y. Lu, Srijon Mukherjee, Michael Gilbert, Li Jing, Vladimir Čeperić, and Marin SoljačićIEEE Transactions on Neural Networks and Learning Systems, 2021
Integration of Neural Network-Based Symbolic Regression in Deep Learning for Scientific DiscoverySamuel Kim, Peter Y. Lu, Srijon Mukherjee, Michael Gilbert, Li Jing, Vladimir Čeperić, and Marin SoljačićIEEE Transactions on Neural Networks and Learning Systems, 2021Symbolic regression is a powerful technique to discover analytic equations that describe data, which can lead to explainable models and the ability to predict unseen data. In contrast, neural networks have achieved amazing levels of accuracy on image recognition and natural language processing tasks, but they are often seen as black-box models that are difficult to interpret and typically extrapolate poorly. In this article, we use a neural network-based architecture for symbolic regression called the equation learner (EQL) network and integrate it with other deep learning architectures such that the whole system can be trained end-to-end through backpropagation. To demonstrate the power of such systems, we study their performance on several substantially different tasks. First, we show that the neural network can perform symbolic regression and learn the form of several functions. Next, we present an MNIST arithmetic task where a convolutional network extracts the digits. Finally, we demonstrate the prediction of dynamical systems where an unknown parameter is extracted through an encoder. We find that the EQL-based architecture can extrapolate quite well outside of the training data set compared with a standard neural network-based architecture, paving the way for deep learning to be applied in scientific exploration and discovery.
2020
- Extracting Interpretable Physical Parameters from Spatiotemporal Systems Using Unsupervised LearningPeter Y. Lu, Samuel Kim, and Marin SoljačićPhysical Review X, 2020
Experimental data are often affected by uncontrolled variables that make analysis and interpretation difficult. For spatiotemporal systems, this problem is further exacerbated by their intricate dynamics. Modern machine learning methods are particularly well suited for analyzing and modeling complex datasets, but to be effective in science, the result needs to be interpretable. We demonstrate an unsupervised learning technique for extracting interpretable physical parameters from noisy spatiotemporal data and for building a transferable model of the system. In particular, we implement a physics-informed architecture based on variational autoencoders that is designed for analyzing systems governed by partial differential equations. The architecture is trained end to end and extracts latent parameters that parametrize the dynamics of a learned predictive model for the system. To test our method, we train our model on simulated data from a variety of partial differential equations with varying dynamical parameters that act as uncontrolled variables. Numerical experiments show that our method can accurately identify relevant parameters and extract them from raw and even noisy spatiotemporal data (tested with roughly 10% added noise). These extracted parameters correlate well (linearly with ) with the ground truth physical parameters used to generate the datasets. We then apply this method to nonlinear fiber propagation data, generated by an ab initio simulation, to demonstrate its capabilities on a more realistic dataset. Our method for discovering interpretable latent parameters in spatiotemporal systems will allow us to better analyze and understand real-world phenomena and datasets, which often have unknown and uncontrolled variables that alter the system dynamics and cause varying behaviors that are difficult to disentangle.
2016
- Extraordinary optical transmission inside a waveguide: spatial mode dependenceOptics Express, 2016
We study the influence of the input spatial mode on the extraordinary optical transmission (EOT) effect. By placing a metal screen with a 1D array of subwavelength holes inside a terahertz (THz) parallel-plate waveguide (PPWG), we can directly compare the transmission spectra with different input waveguide modes. We observe that the transmitted spectrum depends strongly on the input mode. A conventional description of EOT based on the excitation of surface plasmons is not predictive in all cases. Instead, we utilize a formalism based on impedance matching, which accurately predicts the spectral resonances for both TEM and non-TEM input modes.
2013
- Collision dynamics of particle clusters in a two-dimensional granular gasJustin C. Burton, Peter Y. Lu, and Sidney R. NagelPhysical Review E, 2013
In a granular gas, inelastic collisions produce an instability in which the constituent particles cluster heterogeneously. These clusters then interact with each other, further decreasing their kinetic energy. We report experiments of the free collisions of dense clusters of particles in a two-dimensional geometry. The particles are composed of solid CO, which float nearly frictionlessly on a hot surface due to sublimated vapor. After two dense clusters of 100 particles collide, there are two distinct stages of evolution. First, the translational kinetic energy rapidly decreases by over 90% as a “jamming front” sweeps across each cluster. Subsequently, the kinetic energy decreases more slowly as the particles approach the container boundaries. In this regime, the measured velocity distributions are non-Gaussian with long tails. Finally, we compare our experiments to computer simulations of colliding, two-dimensional, granular clusters composed of circular, viscoelastic particles with friction.
-
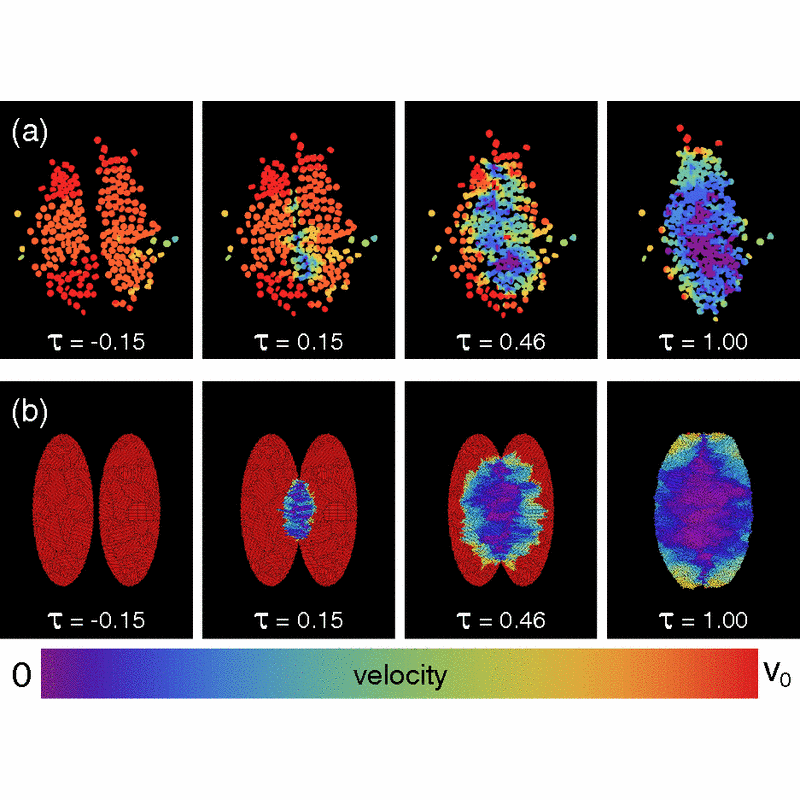 Energy Loss at Propagating Jamming Fronts in Granular Gas ClustersJustin C. Burton, Peter Y. Lu, and Sidney R. NagelPhysical Review Letters, 2013
Energy Loss at Propagating Jamming Fronts in Granular Gas ClustersJustin C. Burton, Peter Y. Lu, and Sidney R. NagelPhysical Review Letters, 2013We explore the initial moments of impact between two dense granular clusters in a two-dimensional geometry. The particles are composed of solid and are levitated on a hot surface. Upon collision, the propagation of a dynamic “jamming front” produces a distinct regime for energy dissipation in a granular gas in which the translational kinetic energy decreases by over 90%. Experiments and associated simulations show that the initial loss of kinetic energy obeys a power law in time , a form that can be predicted from kinetic arguments.







